4.4. Características estadísticas del estimador líder

1) Sesgo. Se dice que un estimador es in sesgado si la Media de la distribución del estimador es igual al parámetro.

Estimadores in sesgados son la Media muestral (estimador de la Media de la población) y la Varianza (estimador de la Varianza de la población):

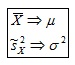
Ejemplo

En una población de 500 puntuaciones cuya Media (m) es igual a 5.09 han hecho un muestreo aleatorio (número de muestras= 10000, tamaño de las muestras= 100) y hallan que la Media de las Medias muestrales es igual a 5.09, (la media poblacional y la media de las medias muestrales coinciden). En cambio, la Mediana de la población es igual a 5 y la Media de las Medianas es igual a 5.1 esto es, hay diferencia ya que la Mediana es un estimador sesgado.

La Varianza es un estimador sesgado. Ejemplo: La Media de las Varianzas obtenidas con la Varianza


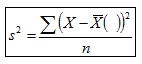
en un muestreo de 1000 muestras (n=25) en que la Varianza de la población es igual a 9.56 ha resultado igual a 9.12, esto es, no coinciden. En cambio, al utilizar la Cuasivarianza



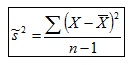
la Media de las Varianzas muestrales es igual a 9.5, esto es, coincide con la Varianza de la población ya que la Cuasivarianza es un estimador insesgado.


2) Consistencia. Un estimador es consistente si aproxima el valor del parámetro cuanto mayor es n (tamaño de la muestra).

Algunos estimadores consistentes son:


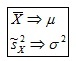
Ejemplo

En una población de 500 puntuaciones cuya Media (m) es igual a 4.9 han hecho tres muestreos aleatorios (número de muestras= 100) con los siguientes resultados:



vemos que el muestreo en que n=100 la Media de las Medias muestrales toma el mismo valor que la Media de la población.

3) Eficiencia. Diremos que un estimador es más eficiente que otro si la Varianza de la distribución muestral del estimador es menor a la del otro estimador. Cuanto menor es la eficiencia, menor es la confianza de que el estadístico obtenido en la muestra aproxime al parámetro poblacional.

Ejemplo

La Varianza de la distribución muestral de la Media en un muestreo aleatorio (número de muestras: 1000, n=25) ha resultado igual a 0.4. La Varianza de la distribución de Medianas ha resultado, en el mismo muestreo, igual a 1.12, (este resultado muestra que la Media es un estimador más eficiente que la Mediana).

ESTIMADORES, MUESTRAS Y CARACTERÍSTICAS DEL ESTIMADOR LIDER

CONCEPTOS

En la estadística tiene un papel destacado la noción de MUESTRA ALEATORIA. Una muestra aleatoria de tamaño n es:

•Una colección de n variables aleatorias

•Todas con la misma distribución

•Todas independientes

Esta definición idealiza la operación de repetir n veces la observación de la misma variable aleatoria, siendo las repeticiones independientes una de otra. La colección de donde extraemos la muestra aleatoria, se denomina POBLACIÓN. Nuestra intención al tomar una muestra, es la de hacer INFERENCIA. Este término lo usamos en estadística para denotar al procedimiento con el que hacemos afirmaciones acerca de valores generales de la población mediante los números que observamos en la muestra.

Ejemplo

Suponga que observamos el proceso de fabricación de las ``bolitas'' que se le ponen al envase de los desodorantes ``roll on''. No todas las bolitas van a tener el mismo diámetro, si escogemos, al azar una bolita, tendremos un valor para el diámetro que es una variable aleatoria. Podemos suponer que los diámetros tienen la distribución normal, debido a nuestra experiencia con el proceso, conocemos que la desviación estándar de la población es de 4 mm (aproximadamente). Pero, también por experiencia, sabemos que el diámetro promedio puede variar por desajuste de la maquinaria productora. De modo que tenemos:

•Una POBLACIÓN, que son todas las bolitas que se producen

•Un PARÁMETRO de la población conocido (o casi) que es la desviación estándar

•Otro PARÁMETRO cuyo valor es desconocido: la media Para tratar de conocer el valor del parámetro que desconocemos, tomamos una MUESTRA de las bolitas. Supongamos que son 100 bolitas en la muestra. Con un instrumento de precisión, y con mucho cuidado, medimos los diámetros de las 100 bolitas de la muestra y calculamos su promedio.