4.5.2. Muestras pequeñas: prueba de Kolmogórov-Smirnov para ajuste de una distribución de probabilidades continua hipotética (en hoja de cálculo o con paquete estadístico)
Prueba de Kolmogorov–Smirnov
En estadística, la prueba de Kolmogórov-Smirnov (también prueba K-S) es una prueba no paramétrica que determina la bondad de ajuste de dos distribuciones de probabilidad entre sí.
La prueba de Kolmogorov-Smirnov se utiliza para probar la bondad del ajuste de una distribución de frecuencia teórica, es decir, si existe una diferencia significativa entre la distribución de la frecuencia observada y la distribución de frecuencia teórica (esperada).
En un post anterior cubrimos el metodo Chi-Cuadrado. La prueba de K-S es similar a lo que hace la prueba de Chi-Cuadrado, pero la prueba K-S tiene varias ventajas:
- Pruebas mas potentes.
- Más fácil de calcular y utilizar, ya que no requiere agrupación de datos.
- La estadística de prueba es independiente de la distribución de la frecuencia esperada. Sólo depende del tamaño de la muestra n.
LA HIPÓTESIS:
H0: La distribución de frecuencia observada es consistente con la distribución de la frecuencia teórica (Buen ajuste).
H1: La distribución de frecuencia observada no es coherente con la distribución de la frecuencia teórica (Bad ajuste).
α = Nivel de significación de la prueba.
H0: La distribución de frecuencia observada es consistente con la distribución de la frecuencia teórica (Buen ajuste).
H1: La distribución de frecuencia observada no es coherente con la distribución de la frecuencia teórica (Bad ajuste).
α = Nivel de significación de la prueba.
Este procedimiento es un test no paramétrico que permite establecer si dos muestras se ajustan al mismo modelo probabilístico (Varas y Bois, 1998).
Es un test válido para distribuciones continuas y sirve tanto para muestras grandes como para muestras pequeñas (Pizarro et al, 1986).
Así mismo, Pizarro (1988), hace referencia a que, como parte de la aplicación de este test, es necesario determinar la frecuencia observada acumulada y la frecuencia teórica acumulada; una vez determinadas ambas frecuencias, se obtiene el máximo de las diferencias entre ambas.
El estadístico Kolmogorov-Smirnov, D, considera la desviación de la función de distribución de probabilidades de la muestra P(x) de la función de probabilidades teórica, escogida Po(x) tal que:
REPORT THIS AD
Dn = max | P(x) – Po(x) |
La prueba requiere que el valor Dn calculado con la expresión anterior sea menor que el valor tabulado Dα para un nivel de significancia (o nivel de probabilidad) requerido. El valor crítico Dα de la prueba se obtiene de la tabla mostrada, en función del nivel de significancia α y el tamaño de la muestra n.
Tabla de valores de Dα en función del nivel de significancia y del tamaño de la muestra:
El procedimiento a seguir en la aplicación práctica de la prueba de Kolmogorov-Smirnov es el siguiente:
- Determinar la frecuencia observada acumulada y la frecuencia téorica acumulada, Po(x) y P(x).
- En cada caso, calcular: Dn = max | P(x) – Po(x) |
Así, Dn es la máxima diferencia entre la función de distribución acumulada de la muestra y la función de distribución acumulada teórica escogida
- Fijar un nivel de probabilidad o de significancia α. Los valores de 0.05 y 0.01 son los más usuales.
- Determinar el valor crítico Dα en la tabla correspondiente.
- Aplica el criterio de decisión:
- Si el valor calculado Dn es menor que el Dα, se acepta la hipótesis nula (Ho) que establece que la serie de datos se ajusta a la distribución teórica escogida.
- Si el valor calculado Dn es mayor que el Dα, se rechaza la hipótesis nula (Ho) y se acepta la hipótesis alternativa (Ha) que establece que la serie de datos no se ajusta a la distribución teórica escogida.
EJEMPLO PRUEBA DE KOLMOGOROV SMIRNOV
Se ha realizado una muestra a 178 municipios al respecto del porcentaje de población activa dedicada a la venta de ordenadores resultando los siguientes valores :
porcentaje
|
nº de municipios
|
menos del 5%
|
18
|
entre el 5 y 10 %
|
14
|
entre 10 y 15%
|
13
|
entre 15 y 20%
|
16
|
entre 20 y 25 %
|
18
|
entre 25 y 30 %
|
17
|
entre 30 y 35 %
|
19
|
entre 35 y 40 %
|
24
|
entre 40 y 45 %
|
21
|
mas de 45%
|
18
|
Queremos contrastar que el porcentaje de municipios para cada grupo establecido se distribuye uniformemente con un nivel de significación del 5%.
Bajo la hipótesis nula cada grupo debiera de estar compuesto por el 10% de la población dado que existen diez grupos . Así podemos establecer la tabla
grupos -variable
|
n0,i
| F0(xi) |
nt,i=n·P(xi)
|
F0(xi)
|  |
menos del 5%
|
18
|
18/178=0,1011
|
17.8
|
17.8/178=0,1
|
0.0011
|
entre el 5y10 %
|
14
|
32/178=0,1798
|
17.8
|
35.6/178=02
|
0,0202
|
entre 10 y 15%
|
13
|
0,2584
|
17.8
|
0,3
|
0,0416
|
entre 15 y 20%
|
16
|
0,3427
|
17.8
|
0,4
|
0,0573
|
entre 20 y 25 %
|
18
|
0,4439
|
17.8
|
0,5
|
0,0561
|
entre 25 y 30 %
|
17
|
0,5393
|
17.8
|
0,6
|
0,0607 max
|
entre 30 y 35 %
|
19
|
0,6461
|
17.8
|
0,7
|
0,0539
|
entre 35 y 40 %
|
24
|
0,7809
|
17.8
|
0,8
|
0,0191
|
entre 40 y 45 %
|
21
|
0,8989
|
17.8
|
0,9
|
0,0011
|
mas de 45%
|
18
|
1
|
17.8
|
1
|
0
|
Siendo la máxima diferencia 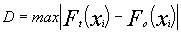=0,0607 y por tanto el estadístico de K-S que compararemos con el establecido en la tabla que será para un nivel de significación de 5% y una muestra de 178 (ir a tabla K-S aqui) 
dado que el estadístico es menor (0,0607) que el valor de la tabla (0,1019) no rechazamos la hipótesis de comportamiento uniforme de los grupos establecidos al respecto de la población activa dedicada a la venta de ordenadores.
=0,0607 y por tanto el estadístico de K-S que compararemos con el establecido en la tabla que será para un nivel de significación de 5% y una muestra de 178 (ir a tabla K-S aqui) 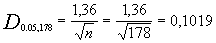dado que el estadístico es menor (0,0607) que el valor de la tabla (0,1019) no rechazamos la hipótesis de comportamiento uniforme de los grupos establecidos al respecto de la población activa dedicada a la venta de ordenadores.
Comentarios
Publicar un comentario